Metoda ta pozwala obliczyc miejsca zerowe funkcji nieliniowych w przedzialach, musi ona jednak spelniac nastepujace warunki:
- funkcja f oraz jej pierwsza i druga pochodna sa ciagle w badanym przedziale <a,b>,
- wewnatrz znajduje sie dokladnie jeden pierwiastek,
- pierwsza i druga pochodna maja staly znak w badanym przedziale <a,b>.
Metoda przebiega nastepujaco: x (0) oraz x (1) wyznaczamy poslugujac sie metoda regula falsi , a nastepne wyznaczamy ze wzoru:

.

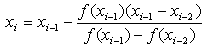Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokladny albo ciag przedzialów zbiezny do pierwiastka. Metoda ta jest znacznie szybciej zbiezna niz metoda regula falsi, ale moze zdarzyc sie równiez przypadek, w którym nie jest zbiezna na przyklad jezeli poczatkowe przyblizenia nie sa dostatecznie blisko rozwiazania.

Do ściągnięcia implementacja metody siecznych.