Metoda ta pozwala obliczyc miejsca zerowe funkcji nieliniowych w przedzialach, musi ona jednak spelniac nastepujace warunki:
- funkcja f oraz jej pierwsza i druga pochodna sa ciagle w badanym przedziale <a,b>,
- wewnatrz znajduje sie dokladnie jeden pierwiastek,
- f(a)*f(b)<0 ,
- pierwsza i druga pochodna maja staly znak w badanym przedziale <a,b>.
Metoda przebiega nastepujaco: badamy znaki funkcji i drugiej pochodnej na krancach badanego przedzialu <a,b> . Za punkt x (0) wybieramy ten koniec przedzialu, w którym funkcja i jej druga pochodna maja równe znaki, a wzór na kolejne punkty wyglada nastepujaco:
![]() .
.
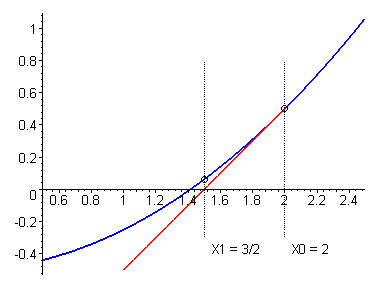
Geometryczna konstrukcje kolejnych przyblizen pierwiastków obrazuje ponizszy wykres (z którego mozna zreszta powyzsze zaleznosci wyznaczyc). Z punktu prowadziwmy styczna do krzywej miejsce przeciecia z osia OX tworzy nowy punkt, z którego prowadzimy kolejna styczna, itd...
Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokladny albo ciag przedzialów zbiezny do pierwiastka. Maksymalny blad i-tego przyblizenia to:

Do ściągnięcia implementacja algorytmu.


